Skip to main content

Leetcode 63. Unique Paths II

Question Description

Original Question: Leetcode 63. Unique Paths II

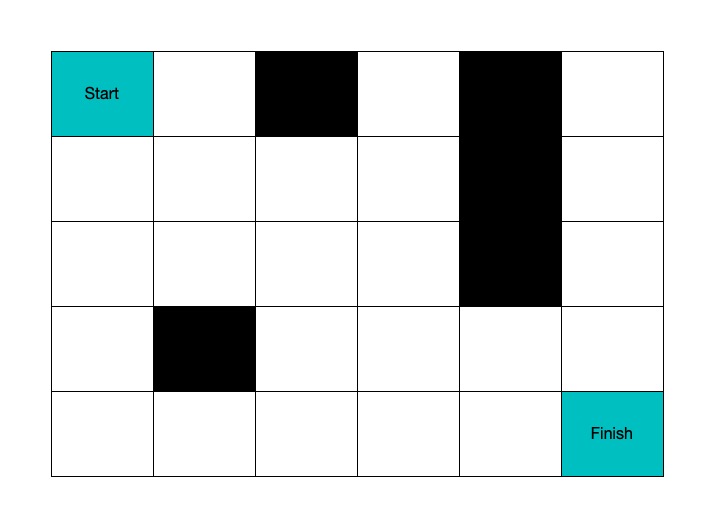
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

Now consider if some obstacles are added to the grids. How many unique paths would there be?

Example:​

Input:
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]
Output: 2
Explanation:
There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right

Solution

class Solution {
    public int uniquePaths(int m, int n) {
        if(m == 0|| n==0) return 0;
        int[][] dp = new int[m][n];
        for(int i = 0; i < m; i++){
            dp[i][n-1] = 1;
        }
        for(int i = 0; i < n; i++){
            dp[m-1][i] = 1;
        }
        for(int j = m-2; j>=0; j--){
            for(int i = n-2; i>=0;i--){
                dp[j][i] = dp[j+1][i] + dp[j][i+1];
            }
        }
        return dp[0][0];
    }
}