Optimal Path Finding Questions
- Unique Path
- Unique Path II
- Minimum Path Sum
- Minimum Falling Path Sum
Question Description
Original Question: Leetcode 62. Unique Paths
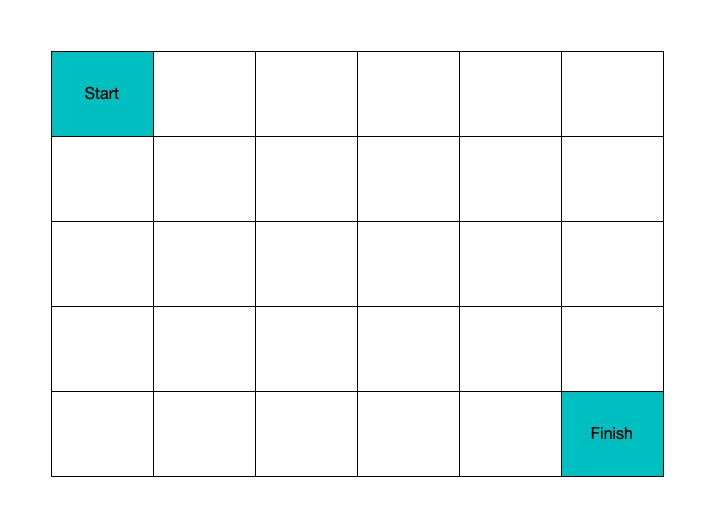
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
Example 1:
Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right
Example 2:
Input: m = 7, n = 3
Output: 28
Solution
- Java
- Python
class Solution {
public int uniquePaths(int m, int n) {
if(m == 0|| n==0) return 0;
int[][] dp = new int[m][n];
for(int i = 0; i < m; i++){
dp[i][n-1] = 1;
}
for(int i = 0; i < n; i++){
dp[m-1][i] = 1;
}
for(int j = m-2; j>=0; j--){
for(int i = n-2; i>=0;i--){
dp[j][i] = dp[j+1][i] + dp[j][i+1];
}
}
return dp[0][0];
}
}
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
if not m or not n:
return 0
paths = [[1]*(n+1)]*(m +1)
for i in range(2,m+1):
for j in range(2, n+1):
paths[i][j] = paths[i-1][j] + paths[i][j-1]
return paths[m][n]
Question Description
Original Question: Leetcode 63. Unique Paths II
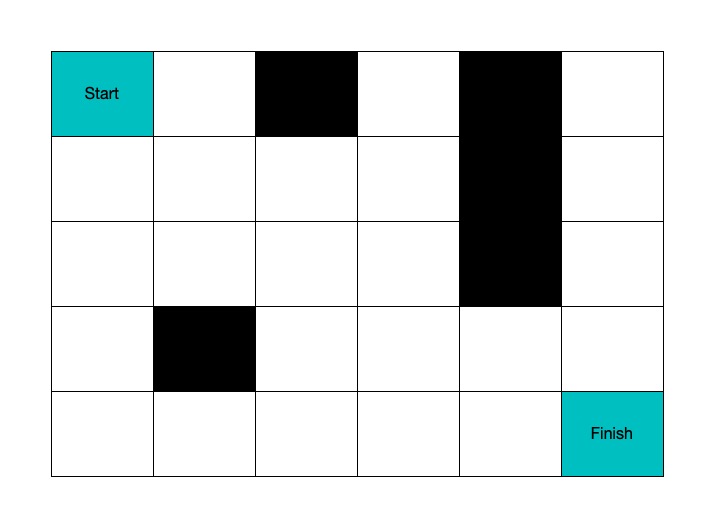
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
Now consider if some obstacles are added to the grids. How many unique paths would there be?
Example:
Input:
[
[0,0,0],
[0,1,0],
[0,0,0]
]
Output: 2
Explanation:
There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right
Solution
- Java
- Python
class Solution {
public int uniquePaths(int m, int n) {
if(m == 0|| n==0) return 0;
int[][] dp = new int[m][n];
for(int i = 0; i < m; i++){
dp[i][n-1] = 1;
}
for(int i = 0; i < n; i++){
dp[m-1][i] = 1;
}
for(int j = m-2; j>=0; j--){
for(int i = n-2; i>=0;i--){
dp[j][i] = dp[j+1][i] + dp[j][i+1];
}
}
return dp[0][0];
}
}
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
if not m or not n:
return 0
paths = [[1]*(n+1)]*(m +1)
for i in range(2,m+1):
for j in range(2, n+1):
paths[i][j] = paths[i-1][j] + paths[i][j-1]
return paths[m][n]
Question Description
Original Question: Leetcode 64. Minimum Path Sum
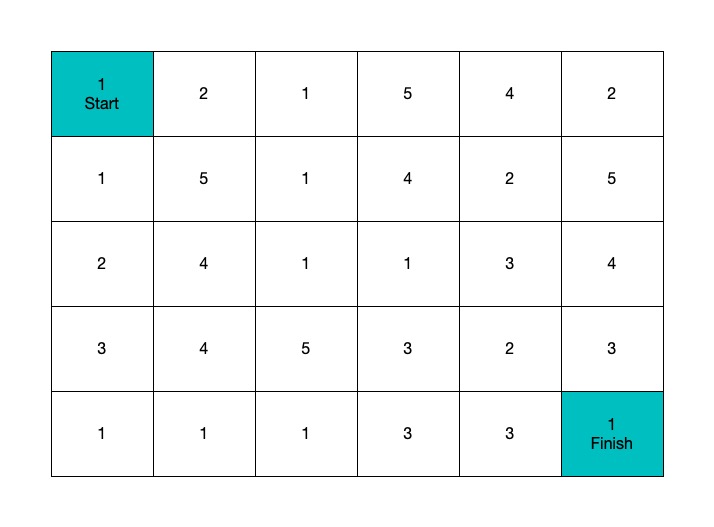
Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.
Note: You can only move either down or right at any point in time.
Example:
Input:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
Output: 7
Explanation: Because the path 1→3→1→1→1 minimizes the sum.
Solution
- Java
- Python
class Solution {
public int minPathSum(int[][] grid) {
if(grid.length == 0 || grid[0].length == 0) return 0;
int[][] dp = new int [grid.length][grid[0].length];
for(int i = 0; i<grid.length; i++){
for(int j = 0; j < grid[0].length; j++){
if(i==0 && j==0) dp[i][j] = grid[0][0];
else if(i==0) {
dp[i][j] = grid[i][j] + dp[i][j-1];
} else if (j == 0){
dp[i][j] = grid[i][j] + dp[i-1][j];
} else {
dp[i][j] = grid[i][j] + Math.min(dp[i-1][j], dp[i][j-1]);
}
}
}
return dp[grid.length-1][grid[0].length-1];
}
}
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
if not grid or not grid[0]:
return 0
m,n = len(grid), len(grid[0])
minSum = [[0 for j in range(n)] for i in range(m) ]
minSum[0][0] = grid[0][0]
for i in range(1,m):
minSum[i][0] = minSum[i-1][0] + grid[i][0]
for j in range(1,n):
minSum[0][j] = minSum[0][j-1] + grid[0][j]
for i in range(1,m):
for j in range(1,n):
minSum[i][j] = min(minSum[i-1][j], minSum[i][j-1]) + grid[i][j]
return minSum[m-1][n-1]
Question Description
Original Question: 931. Minimum Falling Path Sum
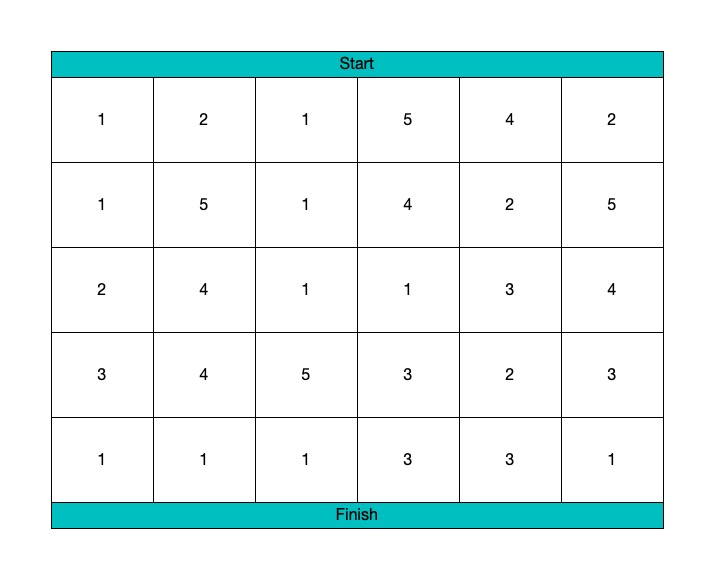
Given a square array of integers A, we want the minimum sum of a falling path through A.
A falling path starts at any element in the first row, and chooses one element from each row. The next row's choice must be in a column that is different from the previous row's column by at most one.
Example:
Input: [[1,2,3],[4,5,6],[7,8,9]]
Output: 12
Explanation:
The possible falling paths are:
- [1,4,7], [1,4,8], [1,5,7], [1,5,8], [1,5,9]
- [2,4,7], [2,4,8], [2,5,7], [2,5,8], [2,5,9], [2,6,8], [2,6,9]
- [3,5,7], [3,5,8], [3,5,9], [3,6,8], [3,6,9]
The falling path with the smallest sum is [1,4,7], so the answer is 12.
Solution
- Java
- Python
class Solution {
public int minFallingPathSum(int[][] A) {
int m = A.length, n = A[0].length;
int[][] dp = new int[m][n];
for(int i = 0; i < n; i++){
dp[0][i] = A[0][i];
}
for(int i = 1; i < m; i++){
for(int j = 0; j < n; j++){
int topLeft = j-1 < 0 ? Integer.MAX_VALUE : dp[i-1][j-1];
int topMid = dp[i-1][j];
int topRight = j+1 >= n ? Integer.MAX_VALUE : dp[i-1][j+1];
dp[i][j] = A[i][j] + Math.min(topLeft, Math.min(topMid, topRight));
}
}
int smallestPath = Integer.MAX_VALUE;
for(int i = 0; i < n; i++){
smallestPath = Math.min(smallestPath, dp[m-1][i]);
}
return smallestPath;
}
}
class Solution:
def minFallingPathSum(self, A: List[List[int]]) -> int:
for i in range(1,len(A)):
for j in range(len(A[0])):
if j == 0:
A[i][j] = min((A[i][j] + A[i - 1][j]), (A[i][j] + A[i - 1][j + 1]) )
elif (j == len(A[0]) - 1):
A[i][j] = min((A[i][j] + A[i - 1][j]), (A[i][j] + A[i - 1][j - 1]) )
else:
A[i][j] = min(A[i][j] + A[i - 1][j],A[i][j] + A[i - 1][j + 1], A[i][j] + A[i - 1][j - 1])
return min(A[len(A) - 1])